Inherente Grenzen

Die Entwicklung der modernen Logik zu Beginn dieses Jahrhunderts hatte das ehrgeizige Ziel, jede erfaßbare Wahrheit unter Benutzung eines logischen Kalküls beweisbar zu machen. So sollte sich jeder überprüfbare Satz mittels einer vorher festgelegten Menge von Axiomen sowie den elementaren logischen Regeln beweisen oder widerlegen lassen. Ein Problem stellte sich jedoch bei Aussagen, die sich auf ihren eigenen Inhalt bezogen. So ist z.B. die Aussage `Diese Aussage ist falsch' mit den Mitteln der Prädikatenlogik sowohl beweisbar als auch widerlegbar, sie bildet also eine Unentscheidbarkeit oder einen Widerspruch. Um derartige (als pathologisch betrachtete) Fälle zu vermeiden, stellten Russell und Whitehead in den `Principia Mathematica' (P.M.) eine `Typentheorie' auf, die durch Hierarchisierung der Aussagenebenen verbot, daß Aussagen auf ihren eigenen Inhalt Bezug nehmen. Der Mathematiker Hilbert forderte daraufhin in dem nach ihm benannten Programm, die Mathematik als vollständiges und widerspruchsfreies System der P.M. zu beweisen. Kurt Gödel bewies aber seinerseits, daß gerade dies nicht möglich ist:

`Im einunddreißigsten Jahr jedoch veröffentlichte Gödel seine Arbeit, die in gewisser Weise Hilberts Programm völlig zerstörte. Sie zeigte nicht nur, daß es in dem axiomatischen System Löcher gab, sondern allgemeiner, daß überhaupt kein axiomatisches System welcher Art auch immer alle Wahrheiten der Zahlentheorie produzieren kann, außer wenn es in sich widerspruchsvoll ist! Und schließlich erwies sich die Hoffnung, die Widerspruchsfreiheit eines Systems wie des der P.M. zu beweisen als eitel: Wenn ein solcher Beweis unter ausschließlicher Verwendung von innerhalb der P.M. verwendeten Methoden gefunden werden konnte, dann - und dies ist eine der verblüffendsten Folgen von Gödels Arbeit - wäre P.M. selbst widerspruchsvoll!'¹²

Der Sachverhalt, daß formale Systeme entweder unvollständig oder widerspruchsvoll sind, ist also fundamental.
Die praktische Bedeutung dieses auf den ersten Blick spitzfindig anmutenden Problems wird deutlich, wenn man zeigt, daß Gödels Satz äquivalent zu einer Aussage ist, die als Konsequenz hat, daß es unmöglich ist, ein Computerprogramm zu erstellen, das mit Sicherheit die Fehlerhaftigkeit eines anderen Programms zu erkennen vermag.¹³ Der Absturz eines Rechners oder elektronischen Bauteils, dem man eine gewisse Komplexität zumutet, ist also prinzipiell niemals vermeidbar. Bedeutsam ist dieses Faktum aber auch für die menschliche Kommunikation, wie wir im zweiten Abschnitt noch sehen werden.

 

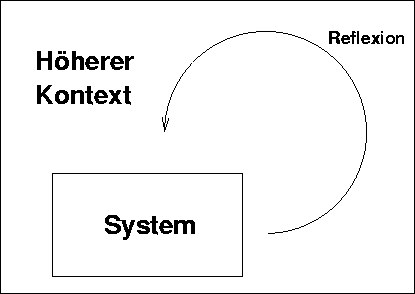
Abbildung: Problem des Rationalismus: Zu jedem System, das Reflexion erlaubt, gibt es gültige reflexive Prozesse, deren Produkt außerhalb dieses Systems liegt.