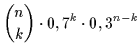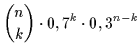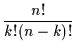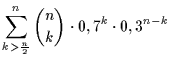

Up: Wahrscheinlichkeiten bei Entscheidungsfindungen
Previous: Einführung und Beispiel
Betrachtet man nun den Fall, daß n Geschworene eine Entscheidung
fällen sollen - weiter unter der exemplarischen Voraussetzung,
daß eine richtige Entscheidung mit  er Wahrscheinlichkeit gefällt
wird. Dabei muß man wie oben alle günstigen Fälle sammeln und ihre
Wahrscheinlichkeiten ausrechnen. Die Wahrscheinlichkeit einer einzelnen
Komposition
er Wahrscheinlichkeit gefällt
wird. Dabei muß man wie oben alle günstigen Fälle sammeln und ihre
Wahrscheinlichkeiten ausrechnen. Die Wahrscheinlichkeit einer einzelnen
Komposition 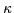 ,
die k richtige Entscheidungen beinhaltet, beträgt:
,
die k richtige Entscheidungen beinhaltet, beträgt:
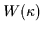 |
= |
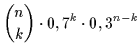 |
(4) |
Wobei
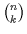 den Binominalkoeffizienten darstellt,
der sich folgendermaßen errechnen läßt:
den Binominalkoeffizienten darstellt,
der sich folgendermaßen errechnen läßt:
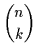 |
= |
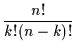 |
(5) |
Der Binomialkoeffizient ergibt sich dabei aus dem folgenden Gedankengang:
Betrachtet man alle möglichen Fälle für ein Ereignis, so muß die Summe ihrer
Wahrscheinlichkeiten 1 ergeben. Also ist die Wahrscheinlichkeit 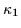 ,
daß ein Geschworener ein falsches oder ein richtiges Urteil fällt,
trivialerweise:
,
daß ein Geschworener ein falsches oder ein richtiges Urteil fällt,
trivialerweise:
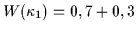 |
= |
1 |
(6) |
Wegen der Multiplikation unabhängiger Ereignisse (s.o.) gilt für n
Geschworene:
| (0,7 + 0,3)n |
= |
1n = 1 |
(7) |
für den im obigen Beispiel verwendeten Fall n=3 ergibt sich, wie bereits
errechnet:
| (0,7 + 0,3)3 |
= |
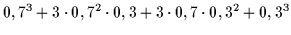 |
(8) |
| |
= |
1 |
(9) |
Die Vorfaktoren, die sich aus der Sortierung gleichnamiger Koeffizienten
für eine Komposition ergeben (im Beispiel also 1, 3, 3 und 1), sind die oben
genannten Binomialkoeffizienten2.
Um nun die Wahrscheinlichkeit für ein richtiges Urteil von n
Geschworenen zu errechnen, muß man wie im Beispiel die Fälle aufsummieren, in
denen die Exponenten der Wahrscheinlichkeit für eine richtige Entscheidung
größer sind als die für eine falsche Entscheidung. Also:
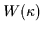 |
= |
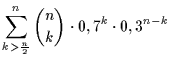 |
(10) |


Up: Wahrscheinlichkeiten bei Entscheidungsfindungen
Previous: Einführung und Beispiel
Tim Paehler
1998-10-30