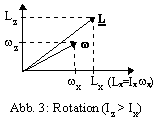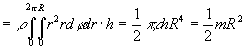Versuch Nr. M 11
Kreisel
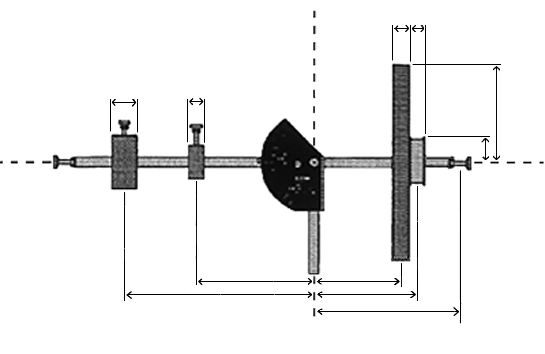
Zubehör siehe Abb.1:
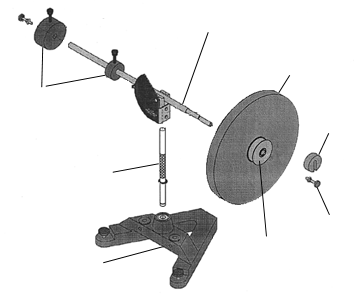

Zusätzlich erhältlich beim Assistenten sind:
Massensatz mit Massenhalterung, zwei Stoppuhren, Schnur, Schieblehre, Zollstock.
Inhalt:
I. Vorbemerkung
II. Grundlagen
III. Qualitative Überlegungen
IV. Vorversuche
V. Theorie der Kreiselbewegungen
Nutation und Präzession
VI. Quantitative Messungen
VII. Theoretische Berechnung der Hauptträgheitsmomente
VIII. Zusatz für Physiker
Was Sie zur Vorbereitung lernen sollten:
Drehmoment, Drehimpuls, Trägheitsmoment, kräftefreier Kreisel, schwerer Kreisel, Präzession und Nutation, Drehimpulssatz. Vergegenwärtigen Sie sich auch die Versuche "Trägheitsmoment" (M6) und "Translations- und Rotationsbewegung" (M7).
Es empfiehlt sich ebenso nachzulesen unter: rotierende Koordinatensysteme, Eulersche Winkel, Eulersche Gleichungssysteme, Kreiselgleichungen, Larmor-Präzession, Larmor-Frequenz.
Literatur:
Bergmann-Schaefer: Lehrbuch der Experimentalphysik, Bd.1: de Gruyter.
Demtröder: Experimentalphysik 1, Mechanik und Wärme: Springer-Verlag.
Falk-Ruppel: Mechanik, Relativität, Gravitation: Springer-Verlag.
French, Anthony P.: Newtonsche Mechanik: de Gruyter.
Kuypers, Friedhelm: Klassische Mechanik: VCH .
I. Vorbemerkung
Ein starrer Körper hat sechs Freiheitsgrade, drei der Translation und drei der Rotation. Unser Kreisel wird in einem Punkt festgehalten, so daß nur drei Freiheitsgrade der Rotation vorhanden sind. Fällt dieser Fixpunkt mit dem Schwerpunkt zusammen, so daß die Gravitationskraft kein Drehmoment (M = dL/dt = 0) ausübt, bewegt sich der Kreisel kräftefrei. Beim kräftefreien Kreisel ist der Drehimpuls L eine raumfeste Größe. Als nicht-kräftefrei bezeichnet man einen Kreisel, wenn ein äußeres Drehmoment M = dL/dt wirkt.
Atome und Atomkerne verhalten sich wie rotierende Magnete. Sie bewegen sich in einem äußeren Magnetfeld wie mechanische Kreisel unter dem Einfluß der Schwerkraft. Die Kenntnis der Kreiselbewegung ist daher nicht nur für das Verständnis von Diskuswurf, Kreiselkompaß, moderner Ballistik und Erdrotation erforderlich, sondern auch für die Wechselwirkung von Protonen, Neutronen und Elektronen, Atomen und Atomkernen mit Magnetfeldern und ist somit für grundlegende physikalische Strukturen und Eigenschaften der Materie von Bedeutung (Aufbau des periodischen Systems, Quantenzahlen, Zeeman-Effekt, Elektronenspin-Resonanz, Kernspin-Resonanz, etc.). Die praktischen Anwendungen reichen von der Auswuchtung von Rädern bis hin zur Kernspin-Resonanz-Tomographie in der Medizin.
II. Grundlagen
Genau wie von Position x und Geschwindigkeit v = dx / dt bei Translationsbewegungen, sprechen wir bei Rotationsbewegungen von Winkelposition f
und Winkelgeschwindigkeit
w
= df
/ dt. x und v sind polare Vektoren, deren Betrag und Richtung klar sind. w
dagegen ist ein axialer Vektor (wie alle Kreuzprodukte, Magnetfelder und durch Drehrichtungen festgelegte Vektoren). w
steht senkrecht auf der von der Rotation beschriebenen Ebene, charakterisiert also deren Lage (im R³) eindeutig. Der Betrag von w
ist, analog zu v, die Winkeländerung pro Zeit; die Richtung, der "rechte" Drehsinn (vgl. Abb 4), ist Konvention.
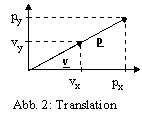
Von Translationsbewegungen sind wir gewohnt, daß Impuls- und Geschwindigkeitsvektor stets gleichgerichtet sind, da die Trägheit eines Körpers in alle Richtungen gleich ist (s. Abb 2).
Es gilt p = mv.
Für den Drehimpuls gilt analog L = I w
(= r ´
p).
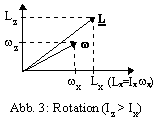
Bei einem beliebigen Körper sind die Trägheitsmomente um verschiedene Drehachsen nicht gleich (s. Abb.3); sie werden durch den Trägheitstensor I beschrieben. Man findet jedoch immer drei aufeinander senkrechte Achsen, die Hauptträgheitsachsen, bei denen der Körper, wenn er um sie gedreht wird, die Hauptträgheitsmomente Ix, Iy und Iz hat.
Da der Rotationssinn irrelevant für die Trägheit ist, ist I symmetrisch, folglich diagonalisierbar mit den Eigenwerten Ix, Iy und Iz und den Eigenvektoren in Richtung der Hauptträgheitsachsen.
Wir beschränken uns auf Kreiselbewegungen eines rotationssymmetrischen Körpers und finden mit der Symmetrieachse (Figurenachse) leicht eine der Hauptträgheitsachsen. Wir benutzen sie als z-Achse des körperfesten Koordinatensystems mit dem Ursprung im Schwerpunkt S (Ix = Iy, s. Abb 2).
Für den Drehimpuls L = (Lx, Ly, Lz) und die Winkelgeschwindigkeit w
= (w
x, w
y, w
z) gilt
L = I w
oder in Komponentenschreibweise:
(1) Lx = Ixw
x , Ly = Iyw
y , Lz = Izw
z .
- h., im allgemeinen Fall haben L, w
und die Figurenachse (z-Achse) auf Grund der unterschiedlichen Trägheitsmomente um verschiedene Drehachsen verschiedene Richtungen (Abb.2). Hieraus resultiert die komplizierte, "torkelnde" Bewegung eines Kreisels.
III. Qualitative Überlegungen
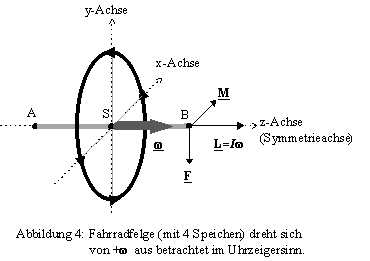
Ergreifen Sie das Vorderrad eines Fahrrades oder betrachten Sie wieder die rotierende Fahrradfelge (Abb. 4), die Sie nun links am Punkt A festhalten, während Sie rechts den Punkt B mit der Kraft F senkrecht nach unten drücken. Das rotierende Rad weicht Ihrer Kraft rechtwinklig (Richtung x-Achse) aus. Dies ist folgendermaßen zu erklären: Das von Ihnen aufgewandte Drehmoment M = d ´
F steht senkrecht auf der Achse (d = AB) und der Kraft F. Nun ist die zeitliche Änderung des Drehimpulses L das Drehmoment M, folglich bewegt sich B in Richtung M = dL/dt.
Durch das ständige senkrechte Ausweichen können Sie sich die Kreisbewegung (Präzession) bei andauernder äußerer Kraft erklären. Auch das Erteilen einer Anfangsgeschwindigkeit zur nutationsfreien Präzession ist so verständlich: Sie erteilen dem Kreisel exakt das Moment entgegen der Gravitationskraft, so daß er nicht "hinunterfällt", was eine Nutationsbewegung einleitete.
IV. Vorversuche
Anhand der Vorversuche sollen Sie sich mit den Bewegungsabläufen vertraut machen. Führen Sie folgende Versuche vor Beginn der quantitativen Messungen durch:
1. Justieren des Kreisels,
2. Antriebsmechanismus,
3. Nutationsbewegung des kräftefreien Kreisels,
4. Präzessionsbewegung,
5. Überlagerung von Nutations- und Präzessionsbewegung,
6. Gegensinnig rotierende Kreiselscheiben.
1. Höhenjustierung des Kreisels, Herstellung des Gleichgewichts
Ziel des Versuchs ist es, die "vertikale Drehachse" (s. Abb. 1) vertikal auszurichten und den Kreisel ins Gleichgewicht zu bringen.
Durchführung :
1) Bringen Sie den Kreisel aus dem Gleichgewicht, indem Sie die Kontergewichte an die vertikale Drehachse schieben.
2) Justieren Sie einen der Schraubfüße der Stativbasis, bis sich die Figurenachse über den anderen Schraubfuß neigt (s. Abb. 6 a).
3) Drehen Sie die Figurenachse um 90 Grad, so daß sie parallel zum anderen Schenkel des Stativfußes ist. (s. Abb. 6 b). Justieren Sie den anderen Schraubfuß solange, bis der Kreisel in dieser Stellung stehen bleibt.
4) Bringen Sie den Kreisel durch Verschieben des 900-g-Gegengewichts und des 40-g-Gegengewichts zum Feinabgleich wieder ins Gleichgewicht.
Hinweis: Plazieren Sie vor der Justierung das Gyroskop gemäß Abb. 12.
2. Antrieb des Kreisels
Ziel des Versuchs ist der sichere Umgang mit dem einfachen Antriebsmechanismus.
Durchführung:
1) Überprüfen Sie, ob der Kreisel sicher montiert ist.
2.a) Um die Kreiselscheibe mit bekannter Energie zu beschleunigen (vgl. VI.), halten Sie die Figurenachse fest, hängen die Schnur mit der Halterung an den hierfür vorgesehenen Dorn und wickeln den Faden sorgfältig auf der Spule auf. Legen Sie bestimmte Massen m auf die Halterung, und lassen Sie diese die Kreiselscheibe über eine bestimmte Strecke h beschleunigen. Hierbei muß die z-Achse des Kreisels in der Waagerechten gehalten werden .
2.b) Für die Vorversuche genügt eine unbekannte Geschwindigkeit der Kreiselscheibe: Wickeln Sie den Faden, wie unter 2.a) beschrieben, auf, halten Sie die Figurenachse fest, und ziehen Sie am Faden, bis der Kreisel die gewünschte Geschwindigkeit erreicht hat.
ACHTUNG: Die Rotationsscheibe kann aus Konstruktionsgründen die vertikale Drehachse berühren. Bitte seien Sie vorsichtig, so daß das Gyroskop nicht beschädigt wird. Bedenken Sie, daß die Kreiselgesetze zu unerwarteten Bewegungen führen!
3. Nutation
Ziel des Versuchs ist die Beobachtung verschiedener Formen der Nutationsbewegung.
Durchführung:
1) Bringen Sie den justierten Kreisel ins Gleichgewicht.
2) Beschleunigen Sie die Kreiselscheibe, und geben Sie dann der Figurenachse einen Stoß. Beobachten Sie die Nutationsbewegung.
4. Präzession
Ziel des Versuchs ist die Demonstration der Wirkung zusätzlicher Drehmomente auf einen präzessierenden Kreisel.
Durchführung:
1) Bringen Sie den justierten Kreisel mit Hilfe der Gegenwichte ins Gleichgewicht.
2) Drehen Sie leicht an der vertikalen Drehachse.
Fassen Sie die Figurenachse am Ende an und bewegen Sie diese in beliebiger Richtung. Erkunden Sie die resultierenden Kräfte, bis Sie die Kreuzprodukte und die durch Dreh- richtungen festgelegten Vektoren (Rechte-Hand-Regeln) vollends erfassen.
3) Stecken Sie eine Zusatzmasse auf die Schraube vor der Rotationsscheibe.
4) Lassen Sie den Kreisel rotieren und geben Sie den Kreisel zur Präzessionsbewegung frei. Erzeugen Sie durch die Vermittlung einer geringen Anfangsgeschwindigkeit in Präzessionsrichtung eine nutationsfreie Präzession.
5) Bremsen und beschleunigen Sie die Präzessionsbewegung durch Drehen der vertikalen Drehachse. Erklären Sie die Bewegung des Kreisels .
5. Überlagerung von Präzession und Nutation
1) Lassen Sie den Kreisel um seine Figurenachse rotieren.
2) Bringen Sie eine Zusatzmasse an, neigen Sie die Figurenachse um 30o (Kreiselscheibe nach oben) und geben Sie dann den Kreisel frei. Die resultierende Bewegung hat die in Abb.7a) dargestellte Form.
3) Halten Sie die rotierende Achse an und geben Sie dem Kreisel nun eine Anfangsgeschwindigkeit in Richtung der Präzessionsbewegung. Die resultierende Nutationsbewegung hat die in Abb.7 b) dargestellte Form.
4) Geben Sie dem Kreisel nun eine Anfangsgeschwindigkeit entgegen der Präzessionsrichtung. Die resultierende Nutationsbewegung hat die in Abb. 7 c) dargestellte Form.
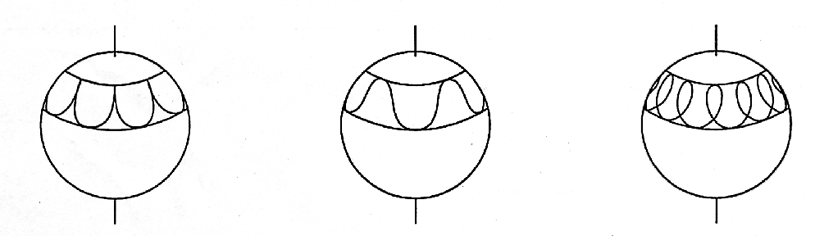
6. Gegensinnig rotierende Kreiselscheiben
Ziel des Versuchs ist die Demonstration der Addition zweier paralleler Drehimpulse.
Durchführung:
1) Befestigen Sie die zweite Rotationsscheibe auf der Figurenachse und bringen Sie den Kreisel mit dem zweiten 900-g-Gegengewicht ins Gleichgewicht.
2) Bringen Sie die beiden Kreiselscheiben auf gleiche Rotationsgeschwindigkeit in entgegengesetzter Richtung, indem Sie die Fäden gegensinnig aufwickeln und dann mit gleichen Massen beschleunigen oder beide Fäden mit einer Hand fassen und so die Kreiselscheiben über die gleiche Strecke mit gleicher Kraft beschleunigen.
3) Erkunden Sie die Eigenschaften dieses Kreisels.
ACHTUNG: Die Kugellager sind von höchster Präzision. Vermeiden Sie bitte jede Berührung der seitlichen Metallabdeckungen - kein Demontieren der ersten Rotationsscheibe - und seien Sie bitte äußerst behutsam beim Aufstecken der zweiten Rotationsscheibe.
V. Theorie der Kreiselbewegungen
1. Nutation (reguläre Präzession) des kräftefreien symmetrischen Kreisels
Ein kräftefreier Kreisel drehe sich mit der Winkelgeschwindigkeit w
z um seine Figurenachse und habe insgesamt den Drehimpuls L = I w
, wobei L = konstant.
1. Fall: L zeigt in Richtung der Figurenachse. Dann bleibt die Figurenachse raumfest, es ist
(2) L = (0, 0, Lz) = (0, 0, Iz w
z).
und folglich w
= w
z (keine Nutation, schlafender Kreisel).
2. (allgemeiner) Fall: L hat eine beliebige Richtung. Für einen beliebigen Zeitpunkt t wählen wir die y-Achse des körperfesten Koordinatensystems senkrecht zu der von L und der z-Achse (Figurenachse) aufgespannten Ebene. Dann gilt für die y-Komponente Ly = Iyw
y = 0 und es ist
(3) L = (Lx, 0, Lz) = (Ix w
x, 0, Iz w
z ).

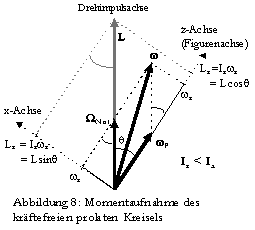
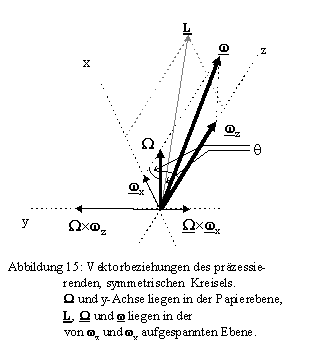
Figurenachse (z-Achse), Drehimpuls L und Winkelgeschwindigkeit w
liegen folglich immer in einer Ebene, so daß w
in den Richtungen von L und der Figurenachse z in Komponentenvektoren zerlegt werden kann (s. Abb. 8).
(4) w
= W
Nut + w
F.
Die Punkte der Figurenachse mit den Ortsvektoren
r = (0, 0, rz) besitzen die Geschwindigkeit
v = w
´
r = W
Nut ´
rz senkrecht zu L und zur
z-Achse. Jeder Punkt der Figurenachse durchläuft folglich einen Kreis senkrecht zum raumfesten Drehimpuls. Die Figurenachse insgesamt bewegt sich auf dem Mantel eines Kegels, dem Nutationskegel, mit der Spitze im Drehpunkt und dem Öffnungswinkel q
zwischen Drehimpuls und Figurenachse. Die Bewegung heißt Nutation oder reguläre Präzession. Ebenso durchläuft auch der Vektor der Winkelgeschwindigkeit einen Kegel, den Rastpolkegel.
Aus Lx = Ixw
x ,Lx = Lsinq
und w
x = W
Nut sinq
(s. Abb.8) folgt für den Betrag von W
Nut
(5) 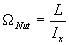 .
.
Für den Betrag der Winkelgeschwindigkeit des Kreisels um seine Figurenachse findet man entsprechend
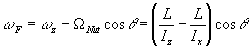
.
Gleichung (5) wird zur Bestimmung des Trägheitsmomentes senkrecht zur Figurenachse benutzt .
2. Präzession des schweren (nicht-kräftefreien) symmetrischen Kreisels
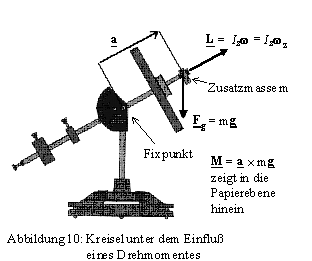
Zur Beschreibung der Bewegung eines Kreisels, auf den ein äußeres Drehmoment wirkt, betrachten wir den einfachen Fall einer nutationsfreien Präzessionsbewegung eines Kreisels
(L in Richtung der Figurenachse, Winkelgeschwindigkeit w
z um die Figurenachse). Es folgt L = Iz w
z (*). Wenn der Kreisel ohne Zusatzmasse kräftefrei ist, dann erzeugt eine Zusatzmasse m im Abstand a vom Fixpunkt das Drehmoment
(6) M = a ´
mg = ¹
0,
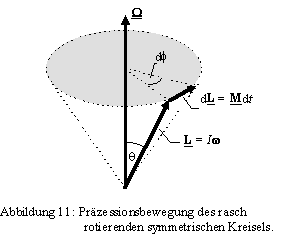
dL steht senkrecht auf der von der Figurenachse und von g aufgespannten Ebene. Der Drehimpuls L in Richtung der Figurenachse bleibt dem Betrag nach konstant und ändert seine Richtung derart, daß die Spitze des Drehimpulsvektors einen Kreis mit der
Winkelgeschwindigkeit W
= df
/dt
durchläuft, wobei dL/dt = rdf
/dt
und r = Lsinq
ist (s.Abb.10).
Dabei bezeichnet q
den Winkel zwischen g und z-Achse. Damit erhält man aus (6):
M = mga sinq
=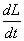 = W
L sinq
= W
L sinq
und für W
(7) mga = IzW
w
z bzw. 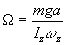 .
.
(*) Diese Beziehung gilt exakt nur für den horizontal rotierenden Kreisel (q
=
p
/2, sinq
= 1) oder näherungsweise für rasch rotierende, symmetrische Kreisel (vgl. dazu VII. Zusatz für Physiker).
Unter dem Einfluß eines Drehmoments M rotiert jeder Punkt der Figurenachse mit der Winkelgeschwindigkeit W
auf einer Kreisbahn senkrecht zu g. Die Figurenachse insgesamt durchläuft den Mantel eines Kegels mit dem Öffnungswinkel q
und der Spitze im Fixpunkt.
VI. Quantitative Messungen
Messung der Hauptträgheitsmomente
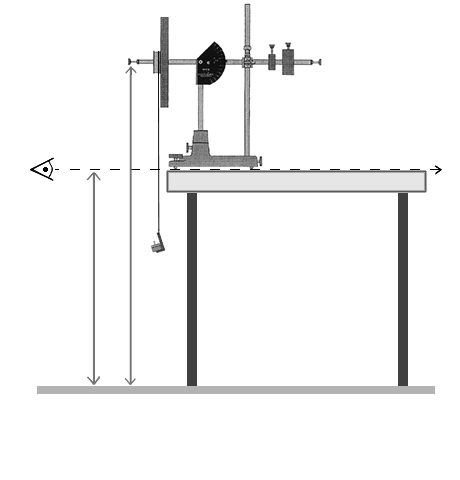
VI. 1. Messung des Trägheitsmomentes der Kreiselscheibe um die Figurenachse (Iz) aus einem Beschleunigungsexperiment:
Die Kreiselscheibe wird durch eine Masse m in Rotation versetzt (s. Abb.12). Das Trägheitsmoment können Sie mit Hilfe des Energiesatzes bestimmen. Dieser Versuch bildet die Fortsetzung des Versuchs "Trägheitsmoment" (M6).
Durchfällt die Masse m die Höhe h, so gilt die Energiebilanz
mgh = ½ mve2 + ½ Iw
e2,
wobei die Endgeschwindigkeit ve des Massenstücks und die erreichte Winkelgeschwindigkeit der Scheibe w
e über ve = RA w
e zusammenhängen (RA = Radius der Spule, vgl. Abb 13). Daraus folgt
(14)  .
.
Durchführung :
1) Fixieren Sie den justierten Kreisel mit Hilfe der Stativstange und Winkelhalterung am Stativfuß und plazieren den Kreisel derart, daß die Spule über die Tischkante hinausragt (siehe Abb. 12).
2) Beschleunigen Sie die Kreiselscheibe mit der Masse m.
- Bestimmen Sie eine Fallhöhe h (Tischhöhe) und messen Sie die erreichte Endwinkelgeschwindigkeit w
e der Kreiselscheibe nach der Beschleunigungsphase, indem Sie die Zeit über mehrere Umdrehungen der Kreiselscheibe messen (w
e=2p
/Te).
Den Anfang der Strecke h können sie über die Tischfläche sehr genau anpeilen.
- Führen Sie diesen Versuch mit mind. 5 verschiedenen Massen (incl. 200g, 150g, 100g und 50g) je drei mal durch. Die Schnur (lS) sollte exakt so lang sein, daß beim Aufschlag der Masse auf dem Boden die Schnur vom Dorn der Spule fällt. Beachten Sie, daß die Masse nicht die Tischkante berührt.
Auswertung:
Tragen Sie 2h/w
e2 gegen 1/mg auf. Zeichnen Sie die Ausgleichsgerade und bestimmen Sie aus deren Steigung das Trägheitsmoment Iz und aus dem Achsenabschnitt den Radius RA der Spule. Bestimmen Sie die Mittelwerte und mittleren Fehler der Endgeschwindigkeiten w
e. Beachten Sie die Masse der Massenhalterung mH = 5,6g.
Die Masse der Schnur sowie die Fehler der Massenstücke brauchen Sie nicht zu berücksichtigen.
VI. 2. Nutation des Kreisels
Das Trägheitsmoment senkrecht zur Figurenachse (Ix) wird nach Gl.(5) bestimmt.
Durchführung
1) Justieren Sie den Kreisel und bringen Sie ihn ins Gleichgewicht.
2) Beschleunigen Sie den Kreisel mit den fünf in Versuch VI.1 benutzten Massen m. Der Drehimpuls liegt dabei in der Figurenachse.
3) Bringen Sie den Kreisel durch einen kurzen ("Karate-") Schlag senkrecht auf die Figurenachse zum Nutieren.
4) Messen Sie die Zeit über mehrere Umläufe der Figurenachse um die raumfeste Drehimpulsachse, und bestimmen Sie daraus die Nutationsgeschwindigkeit W
Nut.
Beachten Sie: durch den Schlag geben Sie dem schlafenden Kreisel mit L = Lz = Iz w
e einen weiteren Drehimpuls Lx senkrecht zur Figurenachse. Der Gesamtdrehimpuls wird vergrößert auf L = Lz +Lx 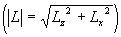 . Da wir die Größe des Impulsübertrages beim Schlag nicht kennen, sollte der Schlag möglichst gering ausfallen (d.h. q
£
5°).
. Da wir die Größe des Impulsübertrages beim Schlag nicht kennen, sollte der Schlag möglichst gering ausfallen (d.h. q
£
5°).
Auswertung:
Übertragen Sie die Endgeschwindigkeiten w
e aus VI.1 und berechnen Sie den jeweiligen Drehimpuls L. Bestimmen Sie aus den fünf experimentellen Werten von W
Nut den Mittelwert und den mittleren quadratischen Fehler für Ix. Entspricht das Verhältnis Iz:Ix dem zu erwartenden Wert?
VI. 3. Präzession des Kreisels
Anhand der Präzessionsgeschwindigkeit W
P des nicht-kräftefreien Kreisels bestimmen Sie das Trägheitsmoment der Kreiselscheibe (Iz) nach Gleichung (7).
Durchführung:
1) Überprüfen Sie die Justierung des Kreisels, und bringen Sie ihn mit Hilfe der Gegengewichte sorgfältig ins Gleichgewicht.
2) Hängen Sie eine Zusatzmasse auf die dafür vorgesehene Schraube. Der Abstand vom Massenmittelpunkt zum Unterstützungspunkt beträgt a = 18,9 cm.
- Beschleunigen Sie den Kreisel mit m = 200g und lassen Sie ihn in der horizontalen Ebene präzessieren (q
= 90°). Eine auftretende Nutation wird verhindert, indem man dem Kreisel eine passende Anfangs- Präzessionsgeschwindigkeit erteilt. Dies ist notwendig, da Gleichung (7) unter der Annahme einer nutationsfreien, horizontalen Präzession hergeleitet wurde.
- Bestimmen Sie die Präzessionsgeschwindigkeit W
P für fünf verschiedene Zusatzmassen mZ. Bei der Messung mit mZ = 153g sollten zwei Umläufe gemessen werden, um die Genauigkeit der Messung zu steigern.
Auswertung:
Übertragen Sie w
e für die Beschleunigung mit m=200g. Tragen Sie W
als Funktion von mgd/w
e auf und bestimmen Sie aus deren Steigung Iz.
VII. Theoretische Berechnung der Trägheitsmomente
1. Berechnung des Trägheitsmomentes der Kreiselscheibe Iz
Die Kreiselscheibe hat eine Gesamtmasse von m = 1735 g. Messen Sie die Radien der Kunststoffscheibe RK und der Aluminiumspule RA mit der Schieblehre, berechnen Sie deren Massen aus dem Literaturwert der Dichte von Aluminium (weitere Daten s. Abb. 13) und hieraus das Trägheitsmoment als Summe der beiden Einzelteile. Diese vereinfachen Sie zu homogenen Zylindern (Rotation um z-Achse, Abb. 14):
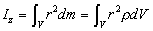
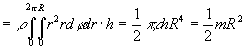
.
Berechnung des Trägheitsmomentes um die vertikale Drehachse Ix
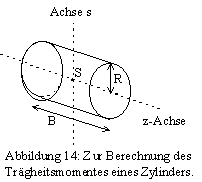
Messen Sie die Abstände der Rotationsscheibe und der Kontergewichte von der vertikalen Drehachse im ausbalancierten Zustand, sowie deren Radien und Breiten. Bitte demontieren Sie nicht die Kreiselscheibe, die nötigen Daten sind angegeben. Das Trägheitsmoment eines Zylinders bei Drehung um eine durch den Schwerpunkt S, parallel zur Kreisfläche verlaufende Drehachse s (Abb.14) beträgt
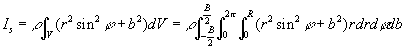
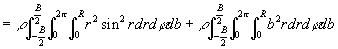
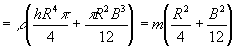 .
.
Nach dem Steinerschen Satz beträgt das Drehmoment bei Parallelverschiebung der Drehachse um den Abstand a (vgl. Abb. 13)
(15) 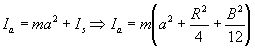 .
.
Sie erhalten das Gesamtträgheitsmoment um die vertikale Drehachse wieder als Summe der Einzelkomponenten, wobei das Trägheitsmoment der z-Achse IAchse = 4,84 gm² beträgt.
Überlegen Sie sich, für welche Komponenten Sie Gleichung (15) oder die des Trägheitsmoments einer dünnen Scheibe (B ®
0) verwenden oder wann Sie eine Konzentration der Masse im Schwerpunkt annehmen können (I = ma²). Vergleichen Sie die Ergebnisse der Messungen untereinander und mit denen der theoretischen Berechnungen.
VIII. Zusatz für Physiker:
Für Gl. (7) nehmen wir an, daß der Drehimpuls des Kreisels in der Figurenachse bleibt. Er setzt sich jedoch aus dem Drehimpuls um die Figurenachse und dem durch die Präzession gegebenen Drehimpuls zusammen. Ein beliebiger Kreiselpunkt besitzt die Winkelgeschwindigkeit
(8) w
= W
+ w
z.
Die xz-Ebene des körperfesten Koordinatensystems wählen wir wieder so, daß die y-Komponente des Drehimpulses verschwindet. Dann ist Ly = Iyw
y = 0 und
L = Ixw
x + Izw
z.
Aufgrund der Präzessionsbewegung des Gesamtsystems mit der Winkelgeschwindigkeit W
gilt für die Drehimpulsänderung
(9) = W
´
L = Ix W
´
w
x + IzW
´
w
z .
Aus Abb. 15 entnimmt man ï
IxW
´
w
x ï
= IxW
w
xcosq
und ï
IzW
´
w
zï
= IzW
w
zsinq
.
Wegen dL/dt ^
W
ist dL/dt ein Vektor in der Horizontalen mit dem Betrag
(10) = -Ix W
w
xcosq
+IzW
w
zsinq
.
Wegen w
x = W
sinq
folgt
(11) = -
Ix W
2 sinq
cosq
+IzW
w
zsinq
= mga sinq
und abweichend von Gl. (7)
(12) mga = Izw
zW
-
Ixcosq
W
2
oder
(13) mga = Izw
zW
(1 -
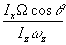 ).
).
Bei horizontaler Figurenachse (cosq
= 0) geht Gl. (12) in Gl. (7) über. Das gilt auch für rasch rotierende Kreisel Izw
z >
>
IzW
.