Translation
Rotation
Masse
m
Trägheitsmoment
![]()
Geschwindigkeit
![]()
Winkelgeschwindigkeit
![]()
Impuls
p
= m vDrehimpuls
L
= I w = r ´ p
Kraft
![]()
Drehmoment
![]()
kinetische Energie
Ekin = 1/2 mv²
kinetische Energie
Ekin = 1/2 mv²
|
Translation |
|
Rotation |
|
|
Masse |
m |
Trägheitsmoment |
|
|
|
|
|
|
|
Geschwindigkeit |
|
Winkelgeschwindigkeit |
|
|
|
|
|
|
|
Impuls
|
p = m v |
Drehimpuls |
L = I w = r ´ p |
|
|
|
|
|
|
Kraft |
|
Drehmoment |
|
|
|
|
|
|
|
kinetische Energie
|
Ekin = 1/2 mv² |
kinetische Energie |
Ekin = 1/2 mv² |
Verschiedene Benennungen
abgeplatteter oder oblater Kreisel (Ix = Iy Iz z. B. Teller, Diskus
gestreckter oder prolater Kreisel z. B. Stift, Flasche
raumfester Kegel: Herpolhodie-, Spur-, Raum-, oder Rastpolkegel
körperfester Kegel: Polhodie-, Gang oder Gangpolkegel
I.1 Einführung in die Theorie der Rotationsbewegungen
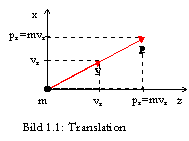
Die Translation eines Körpers der Masse m wird beschrieben durch den
Geschwindigkeitsvektor v = dx/dt.
Der Vektor zeigt zu jedem Zeitpunkt in die Bewegungsrichtung und hat die Länge der Geschwindigkeit (= Streckenänderung pro Zeit). Der Impulsvektor p = mv zeigt immer in Richtung von v, da die Masse (die Trägheit) m eines Körpers in alle Raumrichtungen gleich ist. Führen wir ein Koordinatensystem ein und zerlegen den Impuls- und den Geschwindigkeitsvektor in seine Komponenten pi und vi, haben diese einzelnen Komponenten stets den Proportionalitätsfaktor m (s. Bild 1.1). Dies gilt auch bei der Beschreibung durch ein nicht rechtwinkliges Koordinatensystem.
Je stärker und je länger eine Kraft F = dp/dt auf den Massenpunkt einwirkt, desto mehr ändert sich sein Impuls p. Wirkt keine Kraft F auf den Körper, so bleibt sein Impuls nach Betrag und Richtung konstant.
Die kinetische Energie des Massenpunktes beträgt E = ½ mv2.
Wie im Sprachgebrauch üblich, sagt man: etwas dreht sich um eine
Achse. Die Drehgeschwindigkeit wird beschrieben durch w = dj /dt (= Winkeländerung pro Zeit). Um auch den Sinn der Drehung ("rechtsherum" oder "linksherum") zu beschreiben, führt man -analog zum Geschwindigkeitsvektor v-längs der Drehachse den Winkelgeschwindigkeitsvektor oder Drehvektor
w = dj /dt ein.
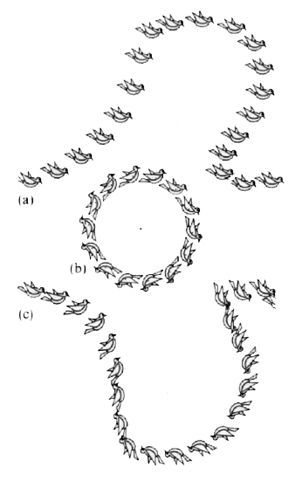
Bild 1.2
a) Translation: die Richtung der Körperachsen bleibt erhalten.
b) reine Rotation.
c) Translation und Rotation.
mit freundlicher Genehmigung des Verlages entnommen aus: Gertsen/Kneser/Vogel, 14. Auflage, S. 66 © Springer, Heidelberg 1986
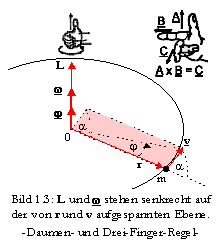
Wenn für Sie die Rotation im Uhrzeigersinn stattfindet, dann betrachten Sie diese in Richtung des Drehvektors +
w (rechtsdrehende Bohrmaschine oder Korkenzieher, Daumenregel der rechten Hand. Betrachten Sie die Rotation in Bild 1.3 "von unten", so schauen Sie in Richtung des Drehvektors).Vektoren solcher Art nennt man Axialvektoren ?? Ausführlich in: Falk/Ruppel, 1973, §24. ??. Während bei der Translationsbewegung die ausgewählte Orientierung des Geschwindigkeitsvektors v = dx/dt (einem polaren Vektor) der normalen Empfindung entspricht, ist die Konvention bei Axialvektoren willkürlich ## A. Sommerfeld und F.Klein definieren in ihren 4 Werken den Drehimpuls in umgekehrter Richtung. Übrigens: Die vektorielle Darstellung hat sich erst in diesem Jahrhundert durchgesetzt. ##. Axialvektoren ändern, im Gegensatz zu polaren Vektoren, bei der Inversion des Koordinatensystems ihr Vorzeichen.
Ein Massenpunkt m, der sich im Abstand r mit der Winkelgeschwindigkeit
w um den Ursprung 0 des Koordinatensystems bewegt, hat die Tangentialgeschwindigkeit v = w × r, sein Drehimpuls ist definiert durch
(1.1)
L = r × p = m (r × v) = m (r × (w × r)).
Der Betrag des Drehimpulses ist |L| = L = m rv sin
a , wobei |r ´ v| = rv sina der Flächeninhalt des von r und v aufgespannten Parallelogramms ist (Bild 1.3).Bewegt sich m auf einer Kreisbahn, stehen r und v stets senkrecht aufeinander und es gilt mit dem
Trägheitsmoment I = mr2;
in Analogie zur Masse bei der Translationsbewegung L = mr2
w = I w .Wirkt kein Drehmoment M = dL/dt = r
´ F auf den Massenpunkt, so bleibt sein Drehimpuls konstant in Betrag und Richtung. Die Konstanz des Drehimpulses sehen Sie prägnant am gut gelagert kardanisch aufgehängten Kreisel (Bild 2.2 Seite 21): Bewegen Sie die Aufhängung des rotierenden Kreisels, so bleiben Drehgeschwindigkeit und Drehachse räumlich konstant - vorausgesetzt, daß Reibungseffekte vernachlässigt werden können.Weitere Beispiele für die Drehimpulskonstanz sind die Pirouette eines Eisläufers ## Äquivalent dazu sind die in fast jedem Lehrbuch zu findenden Drehschemelversuche. weitere interessante Beispiele (Kontraktion von Galaxien) in French, 1995 Kap. 14. ## und die Planetenbahnen: Nach Kepler I sind Planetenbahnen Ellipsen, also liegen v und r in einer Ebene, daher ist die Drehimpulsrichtung zeitlich konstant. Nach Kepler II überstreicht der Ortsradiusvektor r immer eine konstante Fläche pro Zeit, der Betrag des Drehimpulses ist also ebenfalls konstant.
Als Energie ergibt sich: E = ½ mv2 = ½ mr2
w 2 = ½ Iw 2.
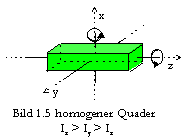
I.1.3 Die Rotation starrer Körper
## Wenn der Abstand zwischen je zwei Massenelementen des Körpers als konstant angenommen werden kann, bezeichnen wir ihn als starren Körper. Während diese Annahme hier bei einem Stück Stahl oder Holz noch vertretbar ist, können wir einen Gummiball oder ein mit Wasser gefülltes Gefäß nicht als starren Körper bezeichnen. ##
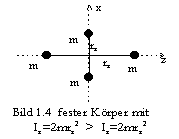
Betrachtet man den in Bild 1.5 dargestellten Quader, so ist sofort ersichtlich, daß eine Rotation mit der Winkelgeschwindigkeit
wx um die x-Achse eine größere Energie beinhaltet als eine Rotation mit gleicher Winkelgeschwindigkeit wz = wx um die z-Achse: Das Trägheitsmoment des Quaders um die z-Achse ist kleiner als das um die x-Achse.Um die Energie um eine Drehachse (etwa der x-Achse) zu berechnen, müssen wir über alle Massenpunkte mi und ihre Abstände zur Drehachse ri summieren (vgl. Bild 1.4) und erhalten für einen Körper
(1.2)

Während wir die Translationsbewegung selbstverständlich in Komponenten aufteilen (s. Bild. 1.1), fällt es schwerer, sich die Rotation eines Körpers in Komponenten vorzustellen. Denken Sie sich eine homogene Kugel (alle durch den Schwerpunkt verlaufenden Drehachsen haben das gleiche Trägheitsmoment) in der Schwerelosigkeit, der Sie zwei Drehstöße um durch den Schwerpunkt verlaufende Achsen erteilen. Sie addieren sich vektoriell analog zu Bild 1.1 (p~L, v~
w , m~I mit Lx=Iw x und Lz=Iw z), und es resultiert eine Drehung w um eine räumlich konstante Achse. Der Drehvektor w w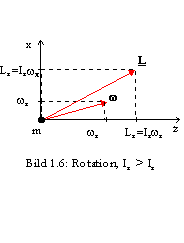
Geben Sie dem Quader zwei Drehstöße, etwa um die zwei in Bild 1.6 eingezeichneten Achsen, werden diese ebenfalls vektoriell addiert. Nun sind jedoch der Impulsvektor L und der Drehvektor
w aufgrund der unterschiedlichen Trägheitsmomente Ix Iy Iz im allgemeinen nicht parallel und der Drehvektor w nicht räumlich konstant. Hieraus resultiert die "Torkelbewegung", die Nutation eines Kreisels.
Um die Rotationen eines starren Körpers in allen Richtungen zu beschreiben, muß das Trägheitsmoment des Körpers für alle möglichen Drehachsen ausgedrückt werden. Dies leistet der Trägheitstensor I , eine für einen Körper charakteristische 3
´ 3 Matrix, mit der gilt: L = I w . Wählen wir die Drehachsen des Quaders in Bild 1.5 (Hauptträgheitsachsen) als Koordinatenachsen (x, y, z), so nimmt I eine einfache Diagonalgestalt an s. (1.5).Für das durch beliebige Drehachsen definierte Koordinatensystem (x’, y’, z’) eines beliebigen Körpers gilt nach der Vektorkorrelation ?? Herleitung z. B. in W. Demtröder, 1994 A.1.5.4. ??
A
´ (B ´ C) =(A C)B - (A B) C und nach (1.1) für das i-te Massenelement des starren Körpers im Abstand ri zur Drehachse
L
i =mi (ri × vi) = mi (ri × (w × ri)) = mi [(ri ri) w - (ri w ) ri].
Den Gesamtdrehimpuls L eines beliebigen starren Körpers mit beliebiger Massenverteilung erhält man durch Integration über alle Massenelemente
(1.3)
Die Zerlegung der Vektoren L und
w in ihre Komponenten liefert für die x’-Komponente von L:
Lx’ =
w x’ ò(x’2+y’2+z’2) dm - ò(w x’x’+w y’y’+w z’z’) x’ dm
=
w x’ ò (r2-x’2) dm - w y’ òx’y’ dm - w z’ òx’z’ dm.
Die anderen Komponenten lassen sich analog berechnen
und mit den Abkürzungen für folgende Ausdrücke
Ix’x’ =
ò (r2 - x’2) dm, Ix’y’ = Iy’x’ = -ò x’y’ dm
(1.4)
Iy’y’ = ò (r2 - y’2) dm, Iy’z’ = Iz’y’ = -ò x’y’ dm
Iz’z’ =
ò (r2 - z’2) dm, Ix’z’ = Iz’x’ = -ò x’y’ dmkönnen wir für L kurz schreiben:
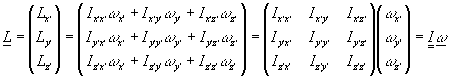
Der Trägheitstensor
I ist für den starren Körper charakteristisch, denn er wird durch die Angabe der Massenverteilung vollständig bestimmt. Seine Koeffizienten hängen ab von der Lage des Ursprungs des körperfesten Koordinatensystems und von der Orientierung dieser Achsen relativ zum Körper.Der Zusammenhang zwischen L und w ist also durch eine lineare Abbildung gegeben, beide Vektoren sind demnach im allgemeinen nicht parallel zueinander. I ist definiert über einem dreidimensionalen Euklidischen Vektorraum V. Da der Rotationssinn irrelevant für das Trägheitsmoment ist, ist die I zugeordnete Matrix symmetrisch ## Da die Komponenten reell sind, ist der Tensor I selbstadjungiert und hermetisch. ## (siehe (1.4)). Die lineare Algebra beweist nun als Hauptachsentheorem ?? Ausführlich in: G. Fischer, 1995, Lineare Algebra, Kap. 10. ??, daß jede endlich dimensionale Matrix ,diagonalisierbar’ ist (oder: auf Hauptachsenform gebracht werden kann), d.h. für die durch die Matrix dargestellte lineare Abbildung gibt es eine Orthonormalbasis, in der ihre Matrix nur auf der Hauptdiagonalen von Null verschiedene Einträge (Eigenwerte) besitzt.
Physikalisch hat das zur Folge, daß es in jedem starren Körper (mindestens) drei zueinander senkrechte Rotationsachsen gibt, für die w und L parallel sind. In dem durch diese Achsen gegebenen Koordinatensystem x, y, z nimmt I Diagonalgestalt ?? Ausführlich in Scheck, 1994. ?? an:
(1.5)
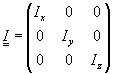
Die Koordinatenachsen dieses körperfesten Koordinatensystems x, y, z werden Hauptträgheitsachsen oder Hauptachsen, die zugehörigen Massenträgheitsmomente (die reellen Eigenwerte Ix, Iy, Iz) Hauptträgheitsmomente genannt. Für den Drehimpuls L = (Lx, Ly, Lz) und die Winkelgeschwindigkeit
w = (w x, w y, w z) gilt
(1.6)
L = I w = Ix w x + Iy w y + Iz w z oder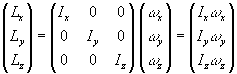 in Matrizenschreibweise.
in Matrizenschreibweise.
(Für den Betrag L eines Vektors L gilt: 2 = L2 = Lx2 + Ly2 + Lz2).
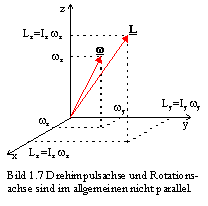
Die Massenträgheitsmomente aller Achsen durch den Ursprung 0 lassen sich also als Linearkombinationen der Hauptträgheitsmomente darstellen.
Nach Bild 1.7 fällt die Richtung von L nur dann mit der von
w zusammen, wenn die Trägheitsmomente Ix, Iy und Iz gleich sind, oder wenn die Drehung um eine der Hauptträgheitsachsen erfolgt, so daß nur eine Komponente der Drehung vorhanden ist. Bild 1.7 entspricht Bild 1.6 eines allgemeinen Körpers in drei Dimensionen.
Mathematisch ist I ein Tensor zweiter Stufe. Zu seiner geometrischen Deutung, dem Trägheitsellipsoiden (der Tensorfläche), gelangt man anschaulich durch den Energieerhaltungssatz:
Für die kinetische Energie des rotierenden Körpers ergibt sich nach ?? Nach Müller / Pouillet, 1929, §5. ?? (1.2):
Ekin = ½
w 2 å mi ri2 = ½ Iw w 2,
wobei I
w das Trägheitsmoment um die augenblickliche Drehachse w ist.Die kinetische Energie ist als quadratische Größe eine Zahl und kein Vektor. Denken wir sie uns dadurch erzeugt, daß wir den Körper um seine Hauptträgheitsachsen mit den entsprechenden Komponenten von
w drehen, dann erhalten wir:
Ekin, x = ½ Ix
wx2, Ekin, y = ½ Iy wy2, Ekin, z = ½ Iz wz2
und als Summe: Ekin = Ekin, x + Ekin, y + Ekin, z
(1.12)
= ½ (Ix w x2 + Iy w y2 + Iz w z2).
Es folgt: 2 Ekin = I
w w 2 = Iw (w x2 +w y2 +w z2 ).
Man erkennt den Zusammenhang von Energie und Impuls:
(1.13)
2 Ekin = w x Lx + w y Ly + w z Lz = w L
mit Lx = Ix
w x, Ly = Iy w y und Lz = Iz w z läßt sich schreiben:
2 Ekin = Ix
w x2 + Iy w y2 + Iz w z2 =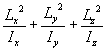
und bei konstanter Energie:
(1.14)
1
Dies ist die Gleichung eines Ellipsoids
![]()
mit den Halbachsen
![]() ,
, 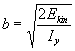 und
und ![]() .
.
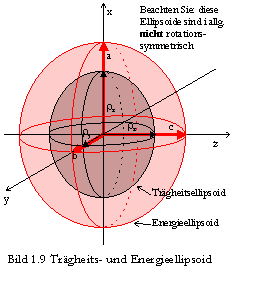
Dieses Ellipsoid nennt man Energieellipsoid ## Poinsot, F., frz. Mathematiker und Physiker, 1777 - 1859, hatte die Idee zu dieser Konstruktion. ##, da es aus der Bedingung konstanter Energie hervorgegangen ist.
Auf diesem Ellipsoid liegt der Endpunkt des Drehvektors
w . Zeichnet man dieses Ellipsoid für den Sonderfall 2 Ekin = 1, so erhält man ein gleichachsig-ähnliches Ellipsoid mit den Halbachsen (Bild 1.9)
![]() ,
, ![]() und
und ![]() , den Trägheitsradien.
, den Trägheitsradien.
Dieses Ellipsoid, das nur mehr von den Trägheitsmomenten des Körpers abhängt, nennt man Trägheitsellipsoid. Die Trägheitsradien liegen in Richtung der Hauptträgheitsachsen und somit, da wir oben die Hauptträgheitsachsen als Koordinatensystem ## Im Koordinatensystem das längs der Hauptachsen definiert ist, sind die Achsen ein Maß des Vektors
r = (r x, r y, r z) , nicht aber des Ortsvektors R. ## verwandt haben, auf den Koordinatenachsen. Selbstverständlich kann das Trägheitsellipsoid auch aus dem allgemeinen, nicht diagonalisierten Trägheitstensor entwickelt werden: Das Trägheitsellipsoid liegt dann schief im Koordinatensystem und die Hauptachsentransformation kann dann als Ausrichtung des Koordinatensystems x’, y’, z’ nach den Halbachsen r x, r y und r z des Ellipsoids verstanden werden ?? Vgl. Demtröder, 1994. ?? .
Bemerkung ?? Nach Schuler, 1951. ?? :
Nicht alle Ellipsoide können Trägheitsellipsoide sein. Es ist, wenn wir das Koordinatensystem mit den Hauptträgheitsachsen zusammenfallen lassen:
Ix
+ Iy = ò (y2 + z2) dm + ò (x2 + z2) dm = ò x2 dm + ò y2 dm + 2 ò z2 dm
<=> Ix + Iy = Iz + 2
ò z2 dmentsprechend gilt: Iy + Iz = Ix + 2
ò x2 dmIz + Ix = Iy + 2 ò y2 dm.
Da die Integrale stets positive Werte haben müssen, ist die Summe von zwei Trägheitsmomenten eines starren Körpers immer größer als das dritte Trägheitsmoment; es sind also nur solche Trägheitsmomente möglich, aus denen sich, als Strecke abgetragen, ein Dreieck konstruieren läßt.
## Die Eulerschen Winkel treten zuerst 1748 in Eulers ‘Introductio in analysin infinitorium’ auf. ##
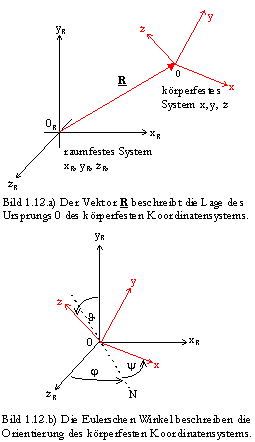
Werfen sie einen Gegenstand durch die Luft, so beschreibt dessen Schwerpunkt die bekannte Wurfparabel. Gleichzeitig rotiert der Körper um seinen Schwerpunkt. Zur Beschreibung dieser Bewegung benötigt man ein im Raum festes Koordinatensystem xR, yR, zR (Inertialsystem), in dem die drei Koordinaten des Ortsvektors R der Translationsbewegung des Schwerpunktes ## Die Wahl des ausgezeichneten Punktes im körperfesten System hängt ab von der jeweiligen Problemstellung. Eulersche Winkel und Drehungsmatrizen explizit in Honerkamp / Römer §4 ## im Raum dargestellt werden. Da die Eigenrotation des Körpers am einfachsten im Hauptachsensystem des Körpers zu beschreiben ist, wählen wir dieses sinnvollerweise als körperfestes Koordinatensystem.
Nun benötigen wir drei weitere Koordinaten zur Beschreibung der Winkellage, d. h. der Orientierung dieses körperfesten Koordinatensystems im Raum — die Eulerschen Winkel.
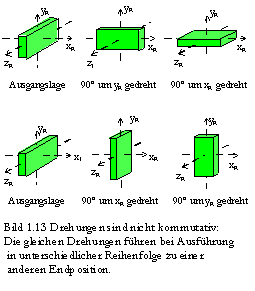
Da Drehungen nicht kommutativ sind (Bild 1.13), müssen die einzelnen Drehachsen exakt vereinbart werden.
Der Übergang vom Raumsystem auf das gedrehte System wird mit drei Drehungen ausgeführt, die nach Bild 1.12b) in folgender Reihenfolge vorzunehmen sind ?? Bild 1.13 und Text nach F. Kuypers, 1993. ??
:
1. Drehung
j um die zR-Achse. Dabei geht die x-Achse in die punktierte ,Knotenlinie’ 0N über.2. Drehung
J um die Knotenlinie 0N. Die inertiale zR-Achse und die körperfeste z-Achse schließen demnach den Winkel J ein.3. Drehung um die z-Achse. Man erhält das körperfeste Koordinatensystem x, y, z.
I.1.7 Rotierende Bezugssysteme
Das mitrotierende Koordinatensystem x, y, z mit den Einheitsvektoren ex, ey und ez rotiert nun mit der Winkelgeschwindigkeit
w gegen das raumfeste Koordinatensystem xR, yR, zR mit den Einheitsvektoren eRx, eRy und eRz, während der Ursprung 0R = 0 für alle Zeiten zusammenfällt (R = 0).
Hat ein Punkt A zur Zeit t im raumfesten System R den Ortsvektor
rR(t) = xR(t) eRx + yR(t) eRy + zR(t) eRz
und die Geschwindigkeit vR(t) = ![]() .
.
Im körperfesten System hat derselbe Punkt A zur gleichen Zeit t den Ortsvektor
r
(t) = rR(t) =x(t) ex + y(t) ey + z(t) ez(wobei r(t) = rR ausdrückt, daß wir denselben Vektor betrachten, der aufgrund der verschiedenen Systeme i. allg. andere Zahlenwerte aufweist.
und die Geschwindigkeit (ohne Berücksichtigung der Rotation des Systems)
v(t) = ![]() .
.
Das körperfeste System rotiert nun mit der konstanten Geschwindigkeit w gegen das Raumsystem. Also gilt
v
R == v + u .
Für die mit der Winkelgeschwindigkeit
w R rotierenden Einheitsvektoren des körperfesten Systems gilt:
![]() ,
, ![]() ,
, ![]()
und für die Geschwindigkeit ergibt das
u = (
w ´ ex) x + (w ´ ey) y +(w ´ ez) z=
w ´ (ex x + ey y + ez z)=
w ´ r.
Wir erhalten als Transformation der Geschwindigkeit des Punktes A, gemessen als vR im Raumsystem und als v im mitrotierenden System
(1.15) vR = v + (
w ´ r).
I.1.8 Die Eulerschen Gleichungen
?? Nach Demtröder, 1994. ??
Um die Bewegung eines Körpers quantitativ beschreiben zu können, muß man die Bewegung des Körpers im raumfesten Koordinatensystem R darstellen.
Die zeitliche Änderung des Drehimpulses dL/dt ist im raumfesten System R, in dem der Beobachter sitzt, gleich dem äußeren Drehmoment ![]() .
.
Im körperfesten Koordinatensystem, dessen Achsen die Hauptachsen des Körpers sind, das also starr mit dem Körper verbunden ist und daher mit der Winkelgeschwindigkeit
w gegen das raumfeste System rotiert, ist die zeitliche Ableitung des Vektors L dann:![]() ,
,
so daß wir die Vektorgleichung
![]() erhalten.
erhalten.
Man beachte, daß hier L im Hauptachsensystem angegeben ist, w jedoch im raumfesten System! Im allgemeinen Fall braucht w in keinem der beiden Systeme zeitlich konstant zu sein. Schreibt man die Gleichung für die Komponenten in Richtung der drei Hauptachsen aus, so erhält man z. B. für die x-Achse:
M = ![]()
= ![]()
= ![]()
= ![]() ,
,
wobei Mx die Komponente des Drehmomentes in Richtung der x-Achse ist.
Entsprechende Gleichungen gelten für die anderen Komponenten.
Insgesamt erhält man die Eulerschen Gleichungen:
![]()
![]()
![]() .
.
Für den Spezialfall des Kugelkreisels (I = Ix = Iy = Iz) gilt: M = I dw /dt
in Analogie zu F = m dv/dt bei der Translation.
Die Eulerschen Gleichungen der kräftefreien Bewegung (Mx = My = Mz = 0) sind nichts anderes als der analytische Ausdruck dafür, daß der Impuls im Raum konstant ist.
Sind äußere Kräfte vorhanden, so sind die Eulerschen Gleichungen der analytische Ausdruck für die Tatsache, daß die Änderungsgeschwindigkeit des Impulses im Raum nach Richtung und Größe gleich dem den äußeren Kräften entsprechenden Drehmoment ist.
Die Differentialgleichungen sind quadratisch in
w und die analytische Lösung ist mit Ausnahme von Spezialfällen schwierig ## F. Klein und A. Sommerfeld führen in ihren vier Werken eine qualitative Diskussion der Gleichungen mit Hilfe elliptischer Integrale durch. ##. Am Ende des Kapitels "Nutation" (I.3.7) schließen sich Lösungen für einen einfachen Spezialfall an.
Die folgenden Kapitel behandeln meist graphische Lösungsmöglichkeiten der Gleichungen für einige Spezialfälle.
Man kann die Gleichungen natürlich auch numerisch ## Ein einfaches BASIC-Programm finden Sie bei: Stauffer, 1989 §1.4.2. ## per Computer lösen.
Oder mit einem ein Gyroskop experimentieren.